sample division problem solving

Word Problems on Division

Word problems on division for fourth grade students are solved here step by step.

Consider the following examples on word problems involving division: 1. $5,876 are distributed equally among 26 men. How much money will each person get? Solution: Money received by 26 men = 5876 So, money received by one man = 5876 ÷ 26 = 226

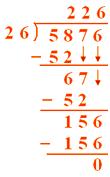
Each man will get $226. 

2.  If 9975 kg of wheat is packed in 95 bags, how much wheat will each bag contain?

Since 95 bags contain wheat 9975 kg Therefore, 1 bag contains wheat (9975 ÷ 95) kg = 105 kg

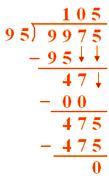
Each bag contains wheat = 105 kg In a problem sum involving division, we have to be careful about using the remainder.

3. 89 people have been invited to a banquet. The caterer is arranging tables. Each table can seat 12 people. How many tables are needed? Solution: To answer this question, we need to divide 89 by 12 89 ÷ 12

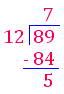
Quotient -  7 

Remainder -  5

If the caterer arranges 7 tables, then 5 people will have no place to sit.  So he needs to arrange 7 + 1 = 8 tables. 

4.  How many hours are there in 1200 minutes? 

Solution: We know that there are 60 minutes in 1 hour.Divide the number of minutes by the number of minutes in 1 hour. We get, divide 1200 by 601200 ÷ 60 = 20

So there are 20 hours in 1200 minutes.

Answer: 20 hours. 

5. A bus can hold 108 passengers. If there are 12 rows of seats on the bus, how many seats are in each row? 

Solution: Total number of passengers = 108

There are 12 rows of seats on the bus.

To find how many seats are there in each row, divide the total number of passengers by the number of rows of seats on the bus.

We get, divide 108 by 12

108 ÷ 12 = 9

Therefore, there are 9 seats in each row.

Answer: 9 seats.

6. Tom had 63 apples. He divides all apples evenly among 9 friends. How many apples did Tom give to each of his friends?

Solution: Total number of apples = 63

There are 9 friends of seats on the bus.

To find how many apples Tom gave to each of his friends, divide the total number of apples by the number of friends. 

We get, divide 63 by 9

Therefore, Tom gives 7 apples to each of his friends.

Answer: 7 Apples

7. Mark baked 195 cookies and divided them equally into 13 packs. How many cookies did Mark put in each packet?

Solution: Total number of cookies = 195

There are 13 packs.

To find how many cookies did Mark put in each packet, divide the total number of cookies by the number of packs.

We get, divide 195 by 13

195 ÷ 13 = 15

Therefore, Mark put 15 cookies in each pack.

Answer: 15 cookies.

9. Nancy needs 5 lemons to make a glass of orange juice. If Nancy has 250 oranges, how many glasses of orange juice can she make?

Solution: Total number of oranges = 250

She needs 5 lemons to make a glass of orange juice.

To find how many glasses of orange juice can Nancy make, divide the total number of oranges by the number of oranges needed for each glass of orange juice.

We get, divide 250 by 5

250 ÷ 5 = 50

Therefore, Nancy can make 50 glasses of orange juice.

Answer: 50 glasses of orange juice.

10. In your classes you counted 120 hands. How many students were at the class?

Solution: Total number of hands = 120

We have 2 hands.

To find how many students were at the class, divide the total number of hands by the number of hands we have.

We get, divide 120 by 2

220 ÷ 2 = 60

Therefore, there were 60 students at the class.

Answer: 60 students.

11. The total train fare for 20 persons is 7540 rupees. What is the fare for 1 person.

12. A milk container can store 8 litres of milk. How many containers are required to stare 6,408 litres of milk?

Capacity of one container = 8 lites of milk

Required number of containers = 6408 ÷  8

Hence, 801 containers are required.

13. A farmer produced 29800 kg of wheat. How many bags will be buy store the wheat if one bag can hold 70 kg?

Produced = 29890 kg

Number of bags needed = 29899 ÷  70

Therefore, 427 bags are needed to hold 29890 kg of wheat.

These are the basic word problems on division.

Questions and Answers on Word Problems on Division:

1. 92 bags of cement can be loaded in a truck. How many such trucks will be needed to load 2208 bags?

Answer: 24  trucks

2. The total train fare for 11 persons was $3850. What was the fare for one person?

Answer:  $350

You might like these

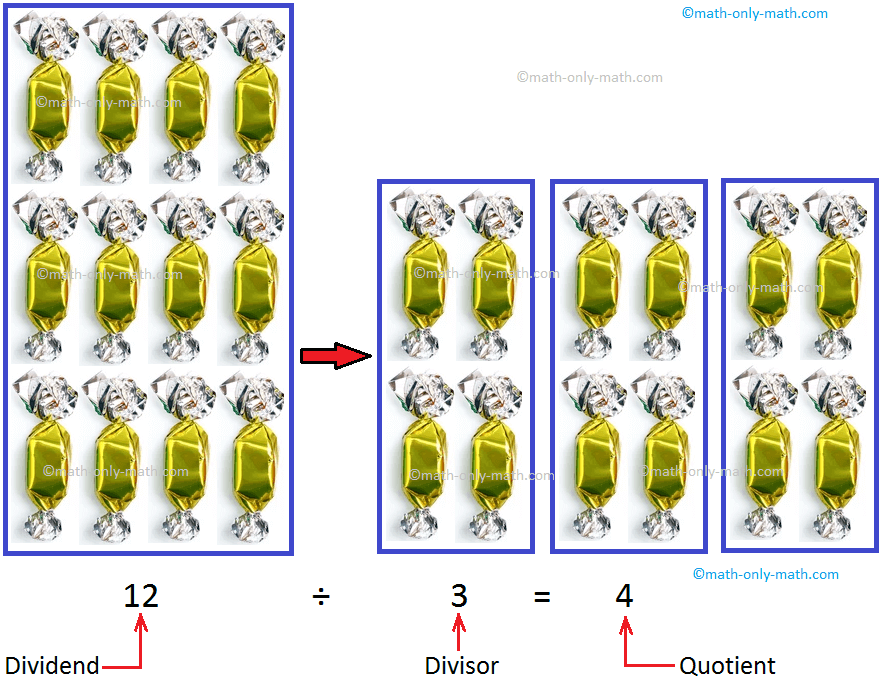
Terms Used in Division | Dividend | Divisor | Quotient | Remainder

The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?

Successor and Predecessor | Successor of a Whole Number | Predecessor

The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also

Worksheets on Comparison of Numbers | Find the Greatest Number

In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:

Number Worksheets | Practice Different Questions on Numbers | Answers

In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which

Comparison of Numbers | Compare Numbers Rules | Examples of Comparison

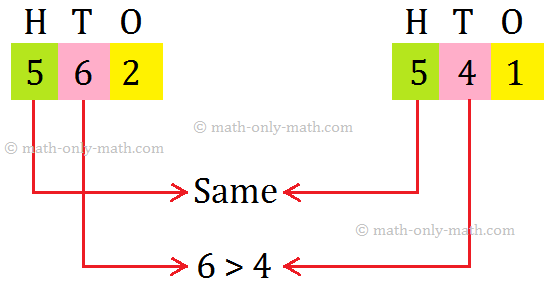
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn

Formation of Numbers | Smallest and Greatest Number| Number Formation

In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,

Formation of Numbers with the Given Digits |Making Numbers with Digits

In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.

Formation of Greatest and Smallest Numbers | Arranging the Numbers

the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the

Place Value | Place, Place Value and Face Value | Grouping the Digits

The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value

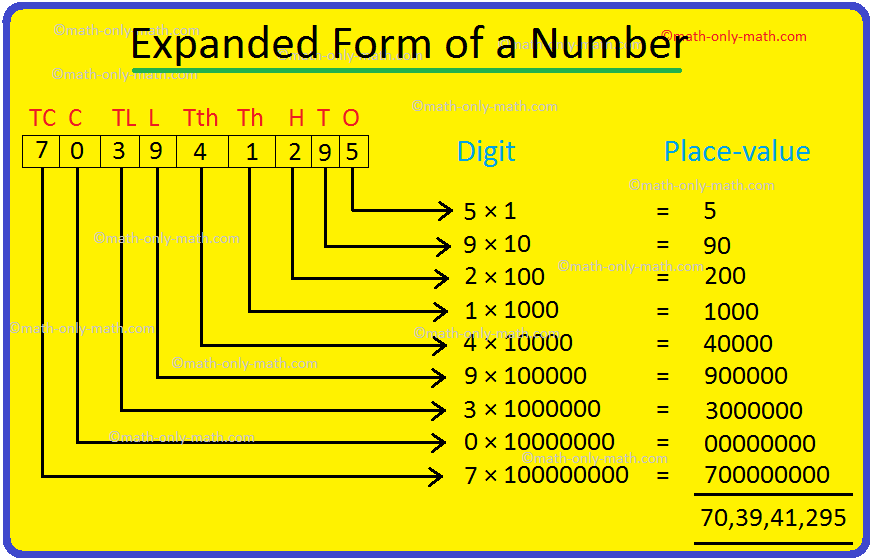
Expanded Form of a Number | Writing Numbers in Expanded Form | Values

We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are

Worksheet on Place Value | Place Value of a Digit in a Number | Math

Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371

Worksheet on Expanded form of a Number | Expanded Form of a Number

Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers

Examples on the Formation of Greatest and the Smallest Number |Example

In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.

Worksheet on Formation of Numbers | Questions on Formation of Numbers

In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students

Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number

Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up

Related Concept

● Word Problems on Addition

● Subtraction

● Check for Subtraction and Addition

● Word Problems Involving Addition and Subtraction

● Estimating Sums and Differences

● Find the Missing Digits

● Multiplication

● Multiply a Number by a 2-Digit Number

● Multiplication of a Number by a 3-Digit Number

● Multiply a Number

● Estimating Products

● Word Problems on Multiplication

● Multiplication and Division

● Terms Used in Division

● Division of Two-Digit by a One-Digit Numbers

● Division of Four-Digit by a One-Digit Numbers

● Division by 10 and 100 and 1000

● Dividing Numbers

● Estimating the Quotient

● Division by Two-Digit Numbers

● Word Problems on Division

4th Grade Math Activities From Word Problems on Division to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Share this page: What’s this?

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

2nd Grade Measurement Worksheets | Measuring Length, Mass and Volume

Nov 19, 24 12:17 AM

2nd Grade Math Practice | Second Grade Math |2nd Grade Math Worksheets

Nov 18, 24 02:23 PM

Worksheet on Addition of Length | Word Problems on Addition of Length

Nov 17, 24 10:29 PM

Worksheet on Addition of Mass | Word problems on Addition of Mass

Nov 17, 24 10:26 PM

Worksheet on Addition of Capacity | Word Problems on Adding capacity

Nov 17, 24 10:19 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled stories
• Sight words
• Sentences & passages
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Math by topic

Download & Print Only $4.10

Division Worksheets

Division worksheets for grade 3 through grade 6.

Our free division worksheets start with practicing simple division facts (e.g. 10 ÷2 = 5) and progress to long division with divisors up to 99. Exercises with and without remainders and with missing divisors or dividends are included.

Choose your grade / topic:

Grade 3 division worksheets, grade 4 mental division worksheets, grade 4 long division worksheets, grade 5 division worksheets, grade 6 division worksheets.

Division facts: drills and practice

Long division: drills and practice

Division flashcards

Topics include:

• Meaning of division & division sentences
• Equal groups
• Division by 2 or 3, 4 or 5, 6 or 7, 8 or 9
• Division facts practice (tables 1-10)
• Division facts practice (tables 1-12)
• Multiplication and division fact families
• Division facts with missing dividend or divisors
• Dividing by 10
• Dividing by 100
• Divide by whole 10s
• Divide by whole hundreds
• Divide 3 or 4 digit numbers by 1 digit numbers (no remainders)
• Division with remainders (1-100)
• Long division: Division facts (1-100), no remainder
• Long division: Division facts (1-100), with remainder
• Division word problems
• Division facts (tables 1-10, 1-12)
• Division facts with missing dividend or divisor
• Divide by 10 or 100
• Divide by whole tens or hundreds
• Divide whole tens or hundreds by 1-digit numbers
• Divide numbers up to 1,000 by 1-digit numbers
• Division with remainders (1-1,000)
• Divide by 10 or 100, with remainders
• Mixed multiplication and division word problems
• Mixed 4 operations word problems
• Division facts in long division form
• 2 digit numbers divided by 1-digit numbers, with / without remainders
• 3 digit numbers divided by 1-digit numbers, with / without remainders
• 4 digit numbers divided by 1-digit numbers, with / without remainders
• Divide 3 or 4-digit numbers by 1-digit numbers mentally
• Division with remainder 1-100, 1-1,000
• Dividing by whole tens or hundreds, with remainders
• Long division with 1-digit divisors, no remainders
• Long division with 1-digit divisors, with remainders
• Long division with 2-digit divisors (10-25, 10-99)
• Missing dividend or divisor problems
• Missing factor problems (solve by long division)
• 1-10,000 divided by 1-digit  numbers, no remainder
• 1-100,000 divided by 1-digit  numbers, with remainder
• Long division by 2-digit divisors

Related topics

Multiplication worksheets

Fractions worksheets

Sample Division Worksheet

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

Join K5 to save time, skip ads and access more content. Learn More

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Kindergarten Thanksgiving
• 1st Grade Thanksgiving
• 2nd Grade Thanksgiving
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• Kindergarten Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Division Worksheets ÷ Hub Page

Welcome to our Division Worksheets hub page.

Here you will find links to our many division worksheet pages, including division facts worksheets, division word problems and long division worksheets.

We also have other division resources including flashcards, division games and online division practice.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

• This page contains links to other Math webpages where you will find a range of activities and resources.
• If you can't find what you are looking for, try searching the site using the Google search box at the top of each page.

Division Learning

Division is often a process which kids often find quite difficult and hard to learn. Kids need to learn what division is before they start formal work on dividing numbers.

Sharing things out, such as counters, between pretend people or cuddly toys is a great way to start your child on their division journey so that they have a basic understanding of what division is. Putting counters into same-size groups is also another way to reinforce division as a model for both sharing and grouping.

When your child is confident with sharing and they have a good understanding of division, they can start learning their division facts and the long division method.

Once they have mastered long division dividing numbers by a single digit, they can start dividing numbers by 2 digits, and begin to learn to divide decimal numbers.

Quicklinks to:

Division Worksheets by Grade

• Understanding Division
• Online Division Practice

Division Facts Worksheets

• Long Division Worksheets & Support
• Dividing Negative Numbers

Division Word Problems

• Division Resources
• Division Games

Second Grade Division

The link below will open the 2nd-grade-math-salamanders website in a new browser window.

• How to do Division Worksheets
• 2nd Grade Division Problems
• Second Grade Division Worksheets

3rd Grade Division

• Division Facts to 10x10 Worksheets
• Long Division Worksheets 3rd Grade
• Division Worksheets Grade 3 Word Problems

4th Grade Division

• Divding by Multiples of 10 and 100 Worksheets
• 4th Grade Long Division Worksheets
• Division Worksheets Grade 4 Word Problems

5th Grade Division

• Decimal Division Facts
• Long Division Worksheets (whole numbers)
• Long Division of Decimal Numbers

Understanding Division Worksheets

Here you will find a selection of Division sheets designed to help your child improve their understanding of what division is.

The sheets introduce the idea of division in terms of sharing and grouping, and designed to be a good practical start to learning about division.

All the free math work sheets in this section are informed by the Elementary Math Benchmarks for 2nd Grade.

• Understanding Division Sheets

Back to Top

Division Flashcards

Here you will find a selection of Division Flashcards designed to help your child learn their Division facts.

Using flashcards is a great way to learn your Math facts. They can be taken on a journey, played with in a game, or used in a spare five minutes daily until your child knows their facts off by heart.

Using these flashcards will help your child to:

• learn their division facts up to 10x10.

All the free Math flash cards in this section are informed by the Elementary Math Benchmarks for 3rd Grade.

• Printable Math Flashcards - Division

Multiplication & Division Times Table Charts

Here you will find a selection of Multiplication/Division Times Table Charts to 10x10 or 12x12 to support your child in learning their multiplication and division facts.

There is a wide selection of multiplication charts including both color and black and white, smaller charts, filled charts and blank charts.

Using these charts will help your child to:

• Learn their multiplication and division facts to 10x10 or 12x12;
• Large Multiplication Chart
• Times Tables Chart to 10x10
• Times Table Grid to 12x12

Division Practice Area

Here is our free division practice area.

If you want to practice your division facts, or take a timed division test, then this is the place for you.

In this area, we cover the following division facts:

• division facts up to 5x5, up to 10x10 or up to 12x12;
• division facts linked to individual tables facts;
• dividing by 10 and 100.
• Division Practice Zone

Here you will find a selection of Mental Division sheets designed to help your child improve their recall of Division Facts and to apply their facts to answer related questions.

Division (and multiplication) Worksheet Generator

Here is our free generator for division (and multiplication) worksheets.

This easy-to-use generator will create randomly generated division worksheets for you to use.

Each sheet comes complete with answers if required.

The areas the generator covers includes:

• Dividing with numbers to 5x5;
• Dividing with numbers to 10x10;
• Dividing with numbers to 12x12;
• Divide with 10s e.g. 120 ÷ 4
• Divide with 100s e.g. 2100 ÷ 3
• Divide with tenths e.g. 2.4 ÷ 6
• Dividing with a single times table;
• Practicing division with selected times tables;

These generated sheets can be used in a number of ways to help your child with their division table learning.

• Division Facts Worksheets (randomly generated)
• Multiplication & Division Worksheets (randomly generated)

Division Facts to 10x10 Sheets (3rd & 4th Grade)

Here you will find a selection of Division sheets designed to help your child learn their Division facts up to 10x10.

Example: if a child knows that 5 x 4 = 20, then they should also know that 20 ÷ 5 = 4 and 20 ÷ 4 = 5.

The sheets are graded so that the division facts start off up to 5x5, progressing on to 10x10 by the end.

Using these sheets will help your child to:

• understand how division and multiplication are related;
• Printable Division Worksheets to 10x10

Division Related Facts 10s and 100s (4th & 5th Grade)

Here you will find a selection of Division sheets designed to help your child learn to use their Division facts up to 10x10 to answer related questions.

Example: if you know that 42 ÷ 6 = 7, then you also know that 420 ÷ 6 = 70 or 420 ÷ 70 = 6, etc.

The sheets are graded so that the related division facts start off easier, then get gradually harder.

• know how to multiply and divide decimals up to 3dp by 10 or 100;
• apply their division facts up to 10x10 to answer related questions.
• Multiply and Divide by 10 100 (decimals)

Division Related Facts Decimals (5th & 6th Grade)

Here you will find a selection of Division sheets designed to help your child learn to use their Division facts up to 10x10 to answer related questions involving decimals.

Example: if you know that 24 ÷ 6 = 4, then you also know that 2.4 ÷ 6 = 0.4 or 2.4 ÷ 0.4 = 6, etc.

• apply their division facts up to 10x10 to answer related questions involving decimals.

Dividing Negative Numbers (6th Grade)

We also have a generator for creating your own division worksheets involving signed integers.

You can choose the values you want and tailor the worksheets to your needs.

• Dividing Negative Numbers (randomly generated)

Long Division Worksheets and Support

Long Division starts properly once kids reach 3rd grade, and after they have a good understanding of what division is, and know their division facts.

Here you will find long division worksheets, starting from dividing a 2 digit number by a single digit, all the way up to dividing a 3 or 4 digit number by two digits.

Long Division Support

We have created a calculator to help you master the long division method.

Just type in the dividend and divisor and let the calculator show you how to work out the long division, step-by-step.

The calculator also gives commentary to show you what is happending at each stage.

• Step by Step Long Division Calculator

Quickinks to ...

• 3rd Grade Long Division
• 4th Grade Long Division
• 5th Grade Long Division
• 6th Grade Long Division

Randomly Generated Long Division Problems Worksheet Generator

Take a look at our long division problems worksheet generators.

This generator will generate your own worksheets from 2-digits by 1-digit to 5-digits by 2-digits.

You can also create your own long division worksheets with money amounts from up to $10 by a single digit to up to $100,000 by 2-digits

You can choose to have remainders or not, and whether to record the remainders as a whole number or fraction.

• Long Division Problems with Answers (randomly generated)
• Long Division with Money (randomly generated)

Long Division 2 Digits by 1 Digit (3rd Grade)

Here you will find a selection of free Division sheets 3rd Grade which are designed to help your child understand how to do long division. The sheets are graded so that the easier ones are at the top.

• divide a 2 digit number by a single digit;
• use remainders when dividing.

Long Division 3 & 4 Digits by 1 Digit (4th Grade)

Here you will find a range of Long Division sheets which are designed to help your child master their Long Division by a single digit.

• use long division to divide a range of numbers by a single digit.

Long Division by 2 Digits (5th Grade)

Here you will find a selection of free Division sheets designed to help your child learn to do 2 digit long division. The sheets are graded so that the easier ones are at the top.

• divide a range of 3,4 and 5 digit numbers by two digits.
• Long Division Worksheets - Dividing by 2 Digits

Long Division by Decimals (6th Grade)

We have some decimal division worksheets with up to 3 decimal places.

There are also some worked examples to show you how.

We have created lots of division word problems for you to solve.

The sheets involve solving division problems in a range of different contexts and involve both sharing and grouping.

These sheets involve solving a range of division problems.

Using this link will open our 2nd Grade Math Salamanders website in a new browser window.

• 2nd Grade Division Worksheets
• Division Sheets Grade 3 Word Problems
• Division Sheets Grade 4 Word Problems

Fun Division Games

Here you will find a range of Free Printable Division Games.

The following games develop the Math skill of dividing in a fun and motivating way.

The following sheets will help your child to:

• learn their Division facts;
• develop their strategic thinking skills.

All the printable Math sheets in this section are informed by the Elementary Math Benchmarks.

• Math Division Games

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return from Division Worksheets page to Math Salamanders Home Page

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Division in Math

Division is a math superpower that breaks down a whole — whether you’re cutting a pizza or divvying up some candy!

Author Christina Levandowski

Expert Reviewer Jill Padfield

Published: August 24, 2023

• Key takeaways
• Division is an opposite game – If you multiply numbers, you can “undo” them using division. It’s multiplication’s opposite function! 
• There’s a few signs to look for – There are three main symbols for division.
• You won’t always get “even Stevens” – Sometimes, you’ll have a little left over. That leftover number is known as the “remainder.”

Table of contents

What is division?

Common symbols and terminology, properties of division, how to divide in 6 easy steps, what is long division, working with remainders.

• Let’s practice together!

Practice problems

Division is one of the most important math skills you’ll practice, helping you to undo multiplication problems or break off parts of a “whole.” We know it looks complicated, but it really isn’t! You just need to know what signs to look for that tell you when division is needed. 

Like addition and subtraction, division uses a few special terms and symbols. Knowing these can help you to work out your problems quickly and correctly. 

We know it sounds complicated right now — but with a little practice and this handy guide, you’ll be flying through your math homework in no time!

Division is a process in math that lets you break down a number into multiple, equal parts. Sometimes, you can cut everything down into whole number parts, and, sometimes, you’ll be left with a little leftover, giving you a decimal or fraction for an answer rather than a whole number. 

You’ll often see division problems vertically, like this:

It can also be written horizontally: 10 ÷ 2, as 10/2 , or using a division bar: 2 ⟌ 10.

No matter how you see it, though, the use for it is always the same. You’re breaking down a number or quantity into smaller pieces. 

Let’s take a look at some key terms that’ll help you build your division skills.

Division is a simple mathematical operation, but there are still a few terms to know to help you find the correct solution. 

Here are the terms you need to know to solve division equations with ease:

➗ — This is known as a division sign, and it tells you that a number needs to be broken down into multiple pieces. 

⟌ — This is the division bar, and it also means to divide. On the outside of the bar, you’ll see the number determining how many pieces are needed from the whole (the divisor), and the dividend on the inside, which is what you’ll be dividing. The answer goes on the top of the bar. 

∕ — This is known as the division slash. Generally, the divisor comes first, and the dividend will appear second.

Important vocabulary

• Divisor – The divisor is the number that is determining how many pieces are needed from the whole. For example: in 15 ÷ 3, three would be the divisor. It’s also the number located outside of the bracket when you see a division bar.
• Dividend – The dividend is the number that’s being divided, and it’s found inside the division bar.
• Quotient – The quotient is your answer, which goes after the equals (=) sign or on the top of the division bar.
• Remainder – In some cases, you’ll have a remainder — which means that the divisor can’t be equally divided into the dividend. The remainder is written to the side of your equation next to the division bar.

Anytime you see the word “property” in math, know that it’s just a rule to remember as you work through your groups of problems. Here are some of the most important properties of division that you need to know: 

• The Division By 1 Property:  If a number is divided by 1, the quotient will always be the original number. 
• The Division By Itself Property: If a number is divided by itself, the quotient will always be 1. 
• The Division By 0 Property: If a number is divided by 0, it’s “undefined” and cannot be solved. 
• The Division Of 0 By (Any) Number Property: If a 0 value is divided by any number, you’ll have 0 as your quotient.

Knowing these helpful properties can help you to do basic operations (like division) confidently. Remember — these are division facts, so these properties will always be true…no matter what problem you’re working to find the quotient to!

Now that you know the terms and properties of your division operation, it’s time to practice your skills. Let’s work the problem below together. 

1. Prepare your equation

We know that the problem above can feel overwhelming — so we want to take this moment to remind you that what we’re doing is breaking down a number into smaller numbers (or smaller groups of numbers). 

First things first, we have to prepare the equation. Feel free to keep it horizontal,  write it vertically, or use a division bar if you’d like. Use whatever method you feel comfortable with. 

Remember: The dividend (15) belongs inside the division bar if you choose to use that method. 

2. Start with the first digit of the dividend from the left

As we begin to divide, we need to start from the first digit from the left (in this case, 1) and ask ourselves: Does the divisor (3) go into 1 at least once? 

The answer here is “no,” so we will then evaluate the first AND second integer (making 15) as a dividend. 

We ask again: Does the divisor (3) go into 15 at least once? 

Now, the answer is “yes” — we just have to count how many times 3 can go into 15, starting our division process.* 

*NOTE: You can do this by using basic arithmetic operations (such as multiplication) to “undo” the problem (i.e., 3 x ? = 15) or counting by threes until you reach 15. 

In our case, 3 goes into 15 a total of five times.

3. Divide it by the divisor and write the answer on top as the quotient

Now that we know that 15 ÷ 3 = 5, it’s time to write it into our equation. Go ahead and write 5 behind the equals sign or standing tall at the top of your division bar. 

4. Subtract the product of the divisor and the digit written in the quotient from the first digit of the dividend

Now, we have to check our work. We have to ask ourselves: What is 5 x 3? Does it equal our dividend? If it does, you’re golden — you’ve done it! 

Do the multiplication, and then subtract your product to ensure that there’s no other steps remaining (like you’d see in the case of a remainder). 

In our example, 15 – 15 = 0…so no remainder or further action is needed.

5. Bring down the next digit in the dividend (if possible)

In other problems, if you did have a three or four digit dividend, you might need to bring down the next digit in the dividend, and determine if your divisor divides that number cleanly. 

You would then repeat the division process, putting your answer over the third or “next” place above the division bar as part of the quotient. 

Next, yo would repeat step 4 to determine if more steps in the division process are needed.

In our example, we don’t have to do this, so we will leave it as is. Good work!

Congratulations! You just broke a large number down into equal, separate parts. It’s time to repeat the process for your other problems. 

Long division is a form of division that’s used to break down larger numbers and will generally repeat steps 1-6 above at least three or more times. 

We’ll work on that stuff later — for now, let’s just focus on mastering the basics!

What happens when you wind up with a little extra left over, you might ask? While it can look pretty scary, it’s simple to solve.

To do this, you’ll repeat steps one through five above until you get a number that cannot continue to be divided evenly. At this point, you’ll do a few additional steps:

• Determine how many times the divisor goes in to the product of your current answer and the divisor. This won’t be a clean number, and that’s OKAY — that’s what your remainder process is for.
• Complete the subtraction steps. After you get your number, complete the subtraction steps and write your answer below the subtraction bar.
• For example: In the case of 16 ➗ 3, we would write the quotient as: 5R1.

When you see that there’s zero left over, or if there is no way for the divisor to divide into the dividend, that means that your problem is solved!

Let’s practice together

• We ask: “How many times can 6 go into 2?” 
• 6 is greater than 2, so we will not be able to put a number over the 2. We then consider, “How many times can 6 go into 20?”
• Well, this is a bit of a challenge! 6 does not go into 20 evenly. 6 x 3= 18, and 6 x 4= 24. So, 6 can go into 20 three times, but it won’t go evenly.
• So, we add the 3 over the 0, above the division bar.
• We put the product of 6 x 3 (our divisor x our quotient) under the dividend and subtract to determine if the a remainder in our difference. 
• There is a remainder of 2. We write our quotient as: 3R2 .

• We know that our divisor is going to be 1, and our dividend (the number being divided) is 5. We identify them, and we put them properly into a division bar. 
• We ask: “How many times can 1 go into 5?” 
• Instead of working the problem counting or using multiplication, we remember the Division By 1 Property. 
• We put 5 at the top of our division bar, since any integer that is divided by 1 will always be itself. 
• There is no remainder for these types of Division By 1 Property problems. We can move on to the next problem.

• We know that our divisor is going to be 2, and our dividend (the number being divided) is 0. We identify them, and we put them properly into a division bar. 
• We ask, “How many times can 2 go into 0?” 
• Instead of working the problem counting or using multiplication, we remember the Division Of 0 By (Any) Number Property. 
• We put 0 at the top of our division bar, since any integer that attempts to divide 0 as a dividend will always result in a quotient of zero. 
• There is no remainder for these types of Division Of 0 By (Any) Number Property problems. We move on to the next problem.

Ready to give it a go?

You’ve done great so far — and you’re well on your way to mastering the art of division. Don’t be afraid to keep trying and make mistakes. 

Practice makes perfect, so we’ve given you a few more problems to practice as you work to perfect your skills. Remember: You can always scroll up to walk through the tutorials and refresh yourself on the terms, placement, and properties you’ll need to solve these correctly. 

By the end of this session, we’re confident that you’ll be ready to claim that A+ on your next math test. You can do it!

Click to reveal the answer.

The answer is 2 .

The answer is 1R6 .

The answer is 4 . 

Parent Guide

The answer is 2.

How did we get here? 

• We identify 4 as the dividend and 2 as the divisor, and place them in the division bar. 
• We ask: “How many times can 2 go into 4?” We determine this using the “count by twos” method, which shows us that 2 goes into 4 a total of two times. 
• We put 2 at the top of our division bar as the quotient, and multiply it by our divisor (2). We then subtract the product of our multiplication from the number to get an answer of 0, which shows us that there is no remainder. You’re done!

The answer is 1R6.

• We identify 8 as our divisor and 14 as our dividend, and place them in the division bar. 
• We ask: “How many times can 8 go into 14?”, as 8 will not go into 1. We determine this using the “count by eights” method, which shows us that 8 goes into 14 just once. 
• We write a 1 in the quotient place above the 4 under the division bar. We then multiply 1 x 8 to get a product of 8, which is placed below the 14 under the division bar. 
• Now, we do the math and subtract 8 from 14. We’ll get 6 as our difference. 
• We then write our quotient as 1R6.

The answer is 4. 

How did we get here?

• We identify 5 as our divisor and 20 as our dividend, and place them in the division bar. 
• We ask: “How many times can 5 go into 20,” as 5 will not go into 2 at all. We determine this using the “count by fives” method, which shows us that 5 can go into 20 cleanly four times. 
• We place a “4” in our quotient place, and multiply 4 x 5 to get a product of 20. This is written under the division bar as a subtraction problem. 
• We subtract 20 – 20, resulting in a difference of 0. 
• This means that 4 is our final quotient with no remainder.

Sign up for the DoodleMath app today!

Turn math into an adventure when you sign up for DoodleMath.

Click here to get started for free!

FAQs about math strategies for kids

We understand that diving into new information can sometimes be overwhelming, and questions often arise. That’s why we’ve meticulously crafted these FAQs, based on real questions from students and parents. We’ve got you covered!

Division is the mathematical process that breaks down a big value into smaller values. 

There are plenty of times you’ll use division in your everyday life. Some of the most common ways might be to break up an even quantity of something, determining how much of an ingredient to use, or grouping up items for use. 

Division is the inverse of multiplication. This means that it naturally undoes any sort of operation that’s done with multiplication. 

The three main parts of division are the divisor, dividend, and quotient. 

Related Posts

Helpful description

Lesson credits

Christina Levandowski

Christina has written for hundreds of clients from small businesses to Indeed.com. She has extensive experience working with marketing strategy and social media marketing, and has her own business creating assets for clients in the space. She enjoys being an entrepreneur and has also started pursuing investment opportunities as time permits.

Parents, sign up for a DoodleMath subscription and see your child become a math wizard!

What we offer

Quick links

All rights reserved. 

Are you a parent, teacher or student?

Get started for free!

Maths information pack

We ask for your contact info so we can send our info pack directly to your inbox for your convenience, exam prep information pack, case studies information pack.

Book a chat with our team

I’m new to Doodle

My school is already using Doodle

Information pack

We ask for your contact info so that our education consultants can get in touch with you and let you know a bit more about doodle., student login, which programme would you like to use.

DoodleMaths

DoodleTables

DoodleEnglish

DoodleSpell

If you’d like to use Doodle’s browser version, please visit this page on a desktop.

To log in to Doodle on this device, you can do so through our apps. You can find out how to download them here:

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Here you will learn about division, including dividing into equal groups, long division, dividing decimals, and dividing fractions.

Students will first learn about division as part of operations and algebraic thinking in 3 rd grade.

What is division?

Division is the process of splitting a number into equal parts or a group of objects into smaller, equal groups. Division is one of the four basic operations (arithmetic operations) and it is the inverse or opposite of multiplication.

To write a division equation, you write the number being divided, the dividend , then a division sign, and then the number that the dividend is being divided by, which is called the divisor . The answer to a division equation is called the quotient .

For example,

Annie wants to split her 28 marbles into equal groups of 4. How many marbles will be in each group?

You would write this as

To solve, you need to divide 28 into 4 equal groups.

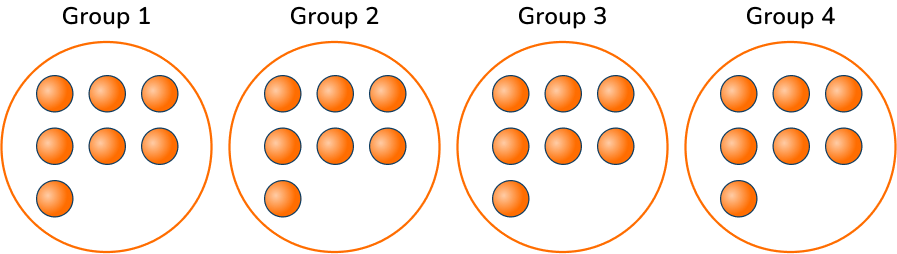
There are 7 in each group, so 28 \div 4=7

You can also solve division facts by writing the equation as an unknown factor problem.

For example, you can solve 28 \div 4 by finding the number that makes 28 when multiplied by 4.

• Long division

To divide larger numbers, you can use the standard algorithm for division, or long division.

Long division is a method of dividing a multi-digit number by another number by repeatedly subtracting multiples of the divisor from the dividend, determining the quotient digit by digit, and bringing down additional digits until the division is complete.

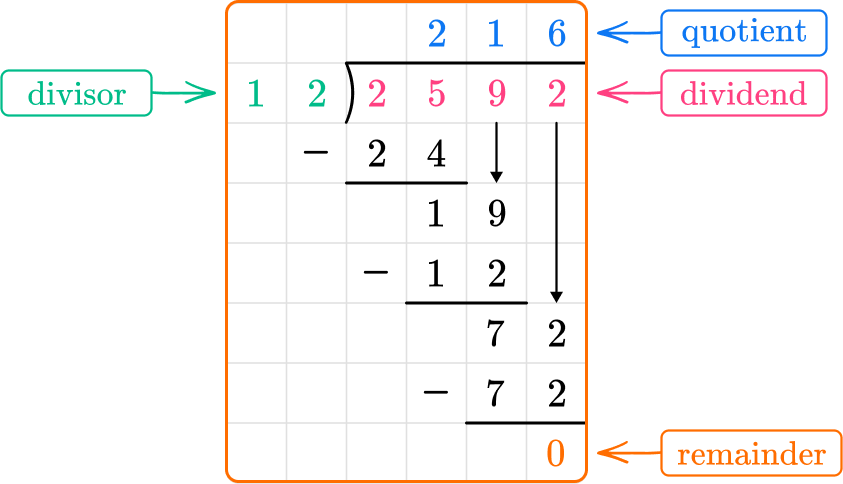
The quotient is shown at the top. There is no remainder, so

If a division problem ends in a remainder, the reminder can be written next to the quotient at the top. For example, if there was a remainder of 2, this could be written as R 2. Remainders can also be written as fractions or decimals.

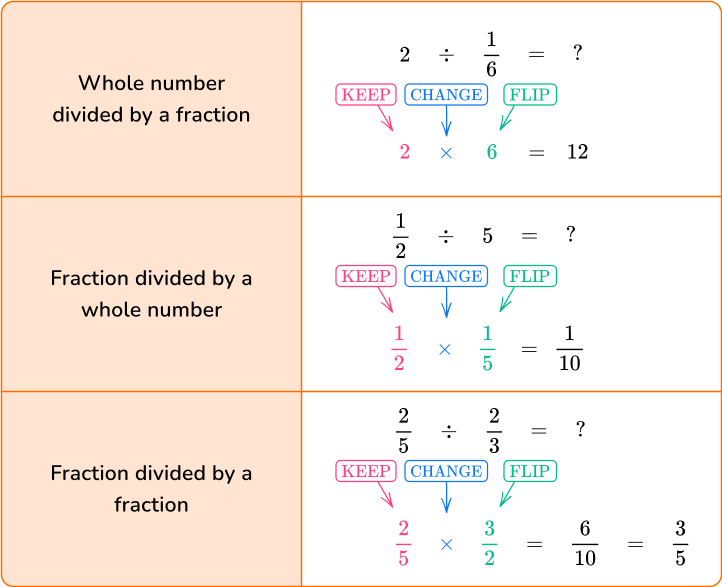
Dividing fractions

To divide fractions, multiply the dividend (the first number in the equation) by the reciprocal of the divisor (second number in the equation). To find the reciprocal of a fraction, switch the numerator and denominator.

Note that a whole number written as a fraction would be the number over 1, so its reciprocal would be 1 over the number. Example: 5=\frac{5}{1} so its reciprocal is \frac{1}{5}.

To remember this process of dividing, think “Keep Change Flip.”

Dividing decimals

You can divide decimals using the standard algorithm, or long division. However, the divisor must be a whole number before you can start the long division process.

If the divisor is a decimal, you must multiply it by a power of 10 to shift the digits so there is no longer a decimal point. Whatever you multiply the divisor by, you must also multiply the dividend by.

a) 8.6 \div 2={?}

Since the divisor is a whole number, you can perform long division. Notice that the decimal point moves straight up to the same place in the quotient.

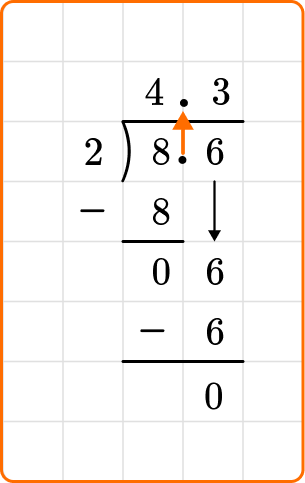
So, 8.6 \div 2=4.3

b) 24.66 \div 1.8={?}

In this example, the divisor, 1.8, is a decimal. Before you can begin the long division process, you will need to multiply 1.8 by a power of 10 so that it will be a whole number. Then you will need to multiply the dividend by that same power of 10.

To make 1.8 a whole number, you can multiply it by 10. Then you also multiply 24.66 by 10. So now, you would use long division to solve 246.6 \div 18.

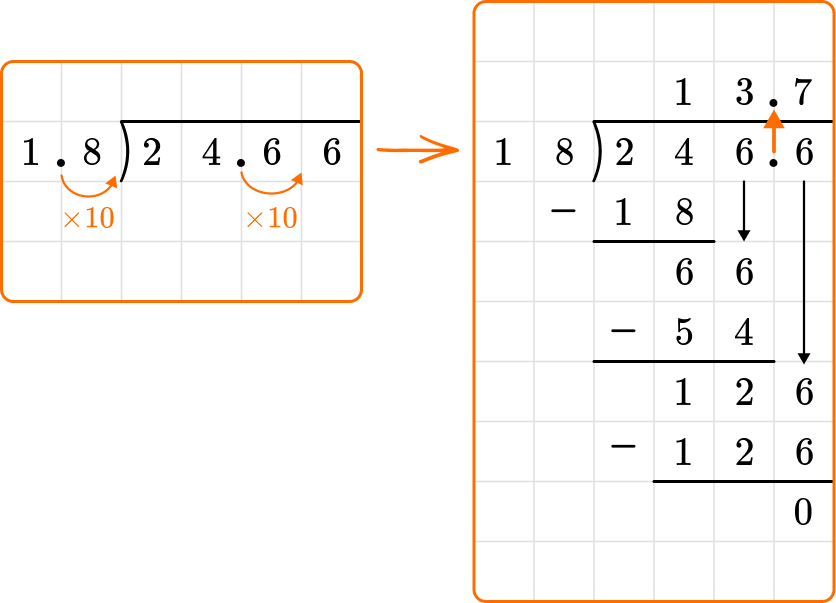
Common Core State Standards

How does this relate to 3 rd grade through 6 th grade math?

• 3rd Grade – Operations and Algebraic Thinking (3.OA.A.2) Interpret whole-number quotients of whole numbers, e.g., interpret 56 \div 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 \div 8.
• 3rd Grade – Operations and Algebraic Thinking (3.OA.B.6) Understand division as an unknown-factor problem. For example, find 32 \div 8 by finding the number that makes 32 when multiplied by 8.
• 4th Grade – Number and Operations in Base Ten (4.NBT.B.6) Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
• 5th Grade – Number and Operations in Base Ten (5.NBT.B.6) Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
• 5th Grade – Number and Operations in Base Ten (5.NBT.B.7) Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
• 5th Grade – Number and Operations—Fractions (5.NF.B.7, 5.NF.B.7a, 5.NF.B.7b, 5.NF.B.7c) Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions. Interpret division of a unit fraction by a non-zero whole number, and compute such quotients. For example, create a story context for (\cfrac{1}{3}) \div 4, and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that (\cfrac{1}{3}) \div 4 = \cfrac{1}{12} because (\cfrac{1}{12}) × 4 = \cfrac{1}{3}. Interpret division of a whole number by a unit fraction, and compute such quotients. For example, create a story context for 4 \div (\cfrac{1}{5}), and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that 4 \div (\cfrac{1}{5}) = 20 because 20 \times (\cfrac{1}{5}) = 4 Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem. For example, how much chocolate will each person get if 3 people share \cfrac{1}{2} lb of chocolate equally? How many \cfrac{1}{3} -cup servings are in 2 cups of raisins?
• 6th Grade – Number and Operations—Fractions (6.NS.A.1) Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. For example, create a story context for (\cfrac{2}{3}) \div (\cfrac{3}{4}) and use a visual fraction model to show the quotient; use the relationship between multiplication and division to explain that (\cfrac{2}{3}) \div (\cfrac{3}{4}) = \cfrac{8}{9} because \cfrac{3}{4} of \cfrac{8}{9} is \cfrac{2}{3}. (In general, (\cfrac{a}{b}) \div (\cfrac{c}{d}) = \cfrac{ad}{bc}.) How much chocolate will each person get if 3 people share \cfrac{1}{2} lb of chocolate equally? How many \cfrac{3}{4} -cup servings are in \cfrac{2}{3} of a cup of yogurt? How wide is a rectangular strip of land with length \cfrac{3}{4} mi and area \cfrac{1}{2} square mi?
• 6th Grade – Number and Operations—Fractions (6.NS.B.2) Fluently divide multi-digit numbers using the standard algorithm.
• 6th Grade – Number and Operations—Fractions (6.NS.B.3) Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.

[FREE] Multiplication and Division Worksheet (Grade 4, 5 and 7)

Use this quiz to check your grade 4, 5 and 7 students’ understanding of multiplication and division. 10+ questions with answers covering a range of 4th, 5th and 7th grade multiplication and division topics to identify areas of strength and support!

How to divide

In order to divide objects into equal groups:

• Identify the total number of objects.
• Determine the number of groups.
• Divide the objects into equal groups.

In order to divide using long division:

Set up the problem.

Divide, multiply and subtract.

Repeat step \bf{2} until the remainder is \bf{0}, or smaller than the divisor and finish to find the quotient.

In order to divide decimals:

If the divisor is a whole number, go to step \bf{3}. If not, decide the power of ten that will make the divisor a whole number.

Multiply both the divisor and the dividend by the same power of \bf{10} .

If the dividend is a decimal number, line up the decimal point of the dividend with the decimal point of the quotient. You may need to include zeros as place holders.

• Perform long division.

In order to divide fractions:

Take the reciprocal (flip) of the divisor (second fraction).

Change the division sign to a multiplication sign.

Multiply the fractions together.

If possible, simplify or convert to a mixed number.

Division examples

Example 1: divide objects into equal groups.

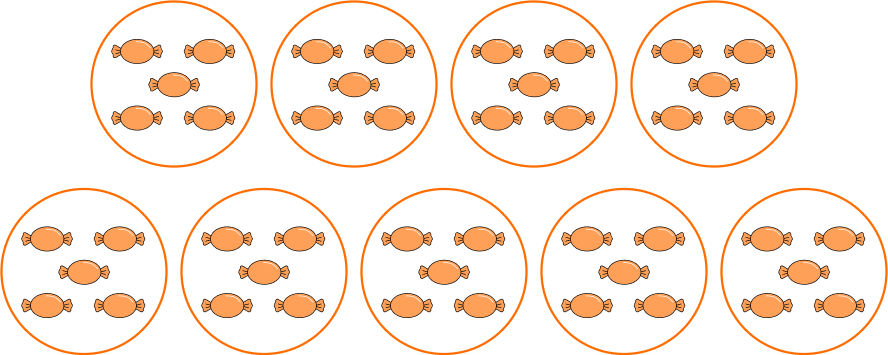
Marcus has 45 pieces of candy. He wants to divide his candy equally between himself and his 8 friends. How many pieces of candy will each person get?

Marcus has a total of 45 pieces of candy.

2 Determine the number of groups.

Marcus is going to divide his candy between himself and 8 friends, so the candy will be divided into 9 equal groups.

3 Divide the objects into equal groups.

45 \div 9=5 in each group

So each person gets 5 pieces of candy.

Example 2: long division (no remainder)

Solve 3211 \div 13 using long division.

When using long division, the numbers are set up under a symbol that is commonly referred to as a “bus stop” or a “house.”

The divisor goes outside of the “house” on the left, and the dividend goes inside the “house.” The quotient will go on top.

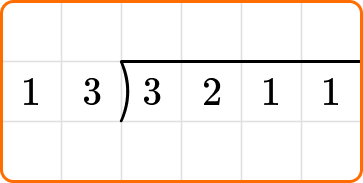
The remainder is zero, so the long division process is done.

That means 3,211 \div 13=247.

Example 3: long division (with remainder)

Solve 857 \div 5 using long division. Write the remainder as a fraction.

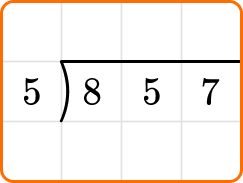
There is a remainder of 2. The directions state to write the remainder as a fraction. To do this, you write the remainder as the numerator and the divisor as the denominator.

So the quotient is 171 \cfrac{2}{5}.

Example 4: dividing decimals (whole number divisor)

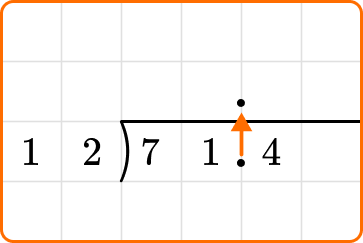
Solve 71.4 \div 12 using long division.

In this division equation, the divisor, 12, is a whole number, so you can skip to step 3.

Do long division.

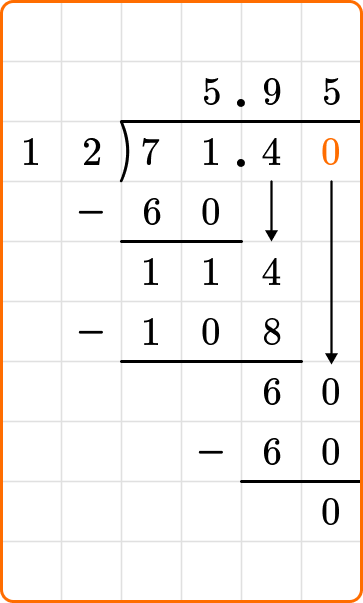
Notice that when getting a remainder when dividing decimals, you add a zero to the end of the dividend to bring down, then continue dividing.

Example 5: dividing decimals (decimal divisor)

Solve 5.13 \div 1.35 using long division.

The divisor, 1.35, is a decimal, so you need to multiply it by a power of 10 to make it a whole number.

To make 1.35 a whole number, you can multiply it by 10^2 or 100. You will also need to multiply the dividend by the same number.

So the new division equation will be 513 \div 135.

Since the dividend and divisor are now whole numbers, there is no decimal point in the dividend to bring up to the quotient. There will only be a decimal point in the quotient if there is a remainder.

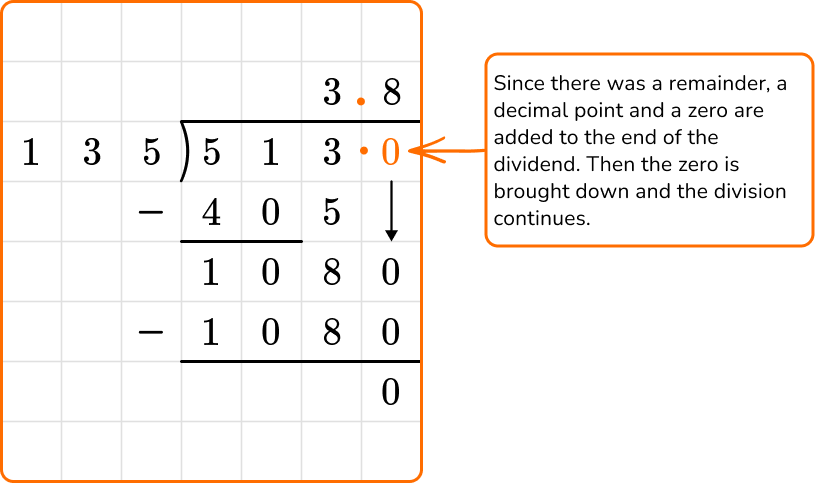
So, 5.13 \div 1.35=3.8

Example 6: whole number divided by a fraction

Solve 6 \div \cfrac{2}{3}

Note that a whole number written as a fraction is the number as the numerator and 1 as the denominator. So the number 6 as a fraction is \cfrac{6}{1}.

\cfrac{6}{1} \times \cfrac{3}{2}=\cfrac{18}{2}

Example 7: fraction divided by a whole number

Solve \cfrac{4}{5} \div 3 .

The fraction is in its simplest form, so the quotient is \cfrac{4}{15}.

Example 8: fraction divided by a fraction

Solve \cfrac{3}{4} \div \cfrac{1}{2}

Teaching tips for division

• Review divisibility rules to assist students with long division. Divisibility rules help with long division by allowing students to more quickly identify potential divisors, reducing the number of attempts needed to find the correct one. For example, “A number is divisible by 2 if it ends in 0, 2, 4, 6, or 8. “
• Teach students different strategies for solving division problems, such as repeated subtraction, equal groups, or using multiplication facts. Encourage them to choose the strategy that works best for them.
• Offer plenty of opportunities for students to practice division through hands-on activities and games, not just worksheets.
• Knowing multiplication tables can help students divide, so provide practice for fluency as needed.

Easy mistakes to make

• Forgetting place value Students may forget to align digits correctly when performing long division, leading to errors in the quotient.
• Forgetting to check for remainders Students may forget to check for remainders or may incorrectly interpret them.

Related multiplication and division lessons

• Multiplication and division
• Multiplicative comparison
• Multiplying multi digit numbers
• Dividing multi digit numbers
• Multiplying and dividing integers
• Negative times negative (coming soon)
• Negative numbers
• Multiplying and dividing rational numbers (coming soon)

Practice division questions

1. Johnny has 30 marbles. He divided them evenly between 6 jars. How many marbles are in each jar? Which model represents this problem?

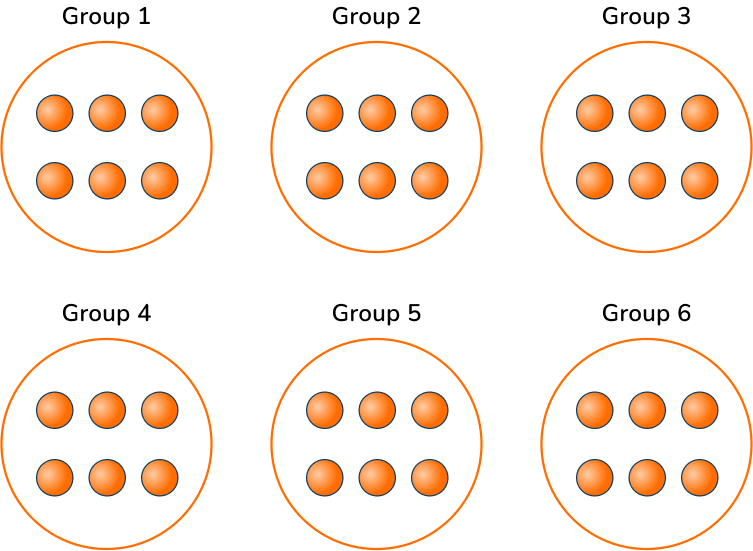
In this word problem, you have a total of 30 objects being divided into 6 groups, so you need to solve 30 \div 6.

The model that shows 6 groups with 5 circles in each group is correct.

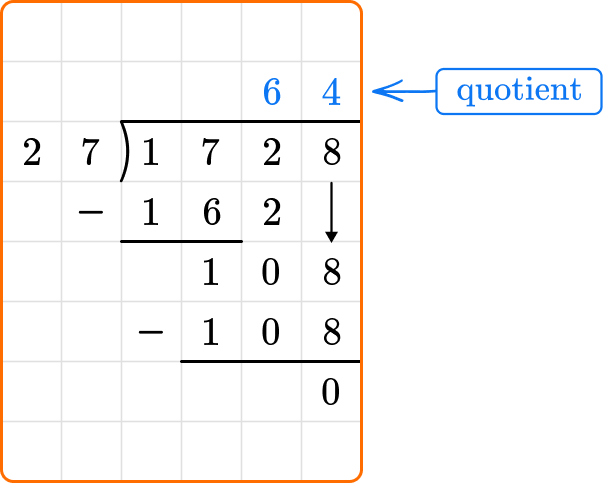
2. Solve 1728 \div 27 .

You can find the quotient using long division.

3. Solve 893 \div 12. Write the remainder as a fraction.

First, use long division to solve. When doing so, you get a remainder of 5. To include the remainder in the quotient as a fraction, you write the remainder as the numerator and the divisor as the denominator.

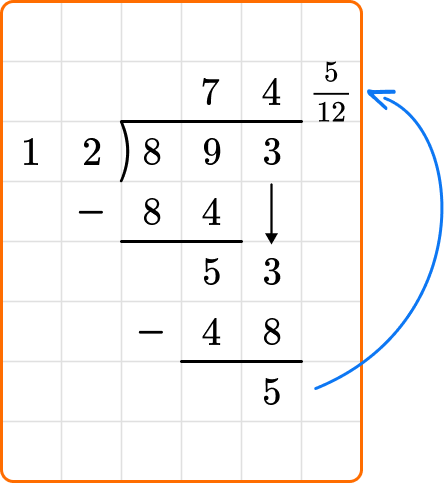
Therefore, 893 \div 12=74 \cfrac{5}{12}

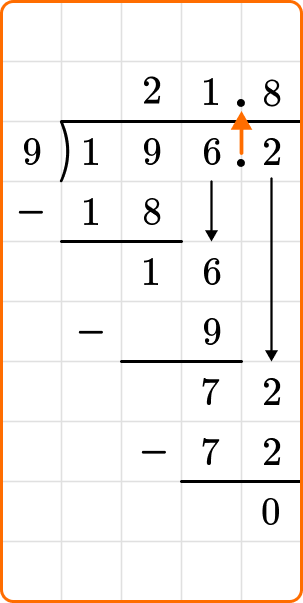
4. Solve 196.2 \div 9 .

This division problem has a decimal, which is the dividend. The divisor is a whole number, however, so you can jump right into the long division process to solve. The decimal point will be placed in the quotient in the same place as the dividend.

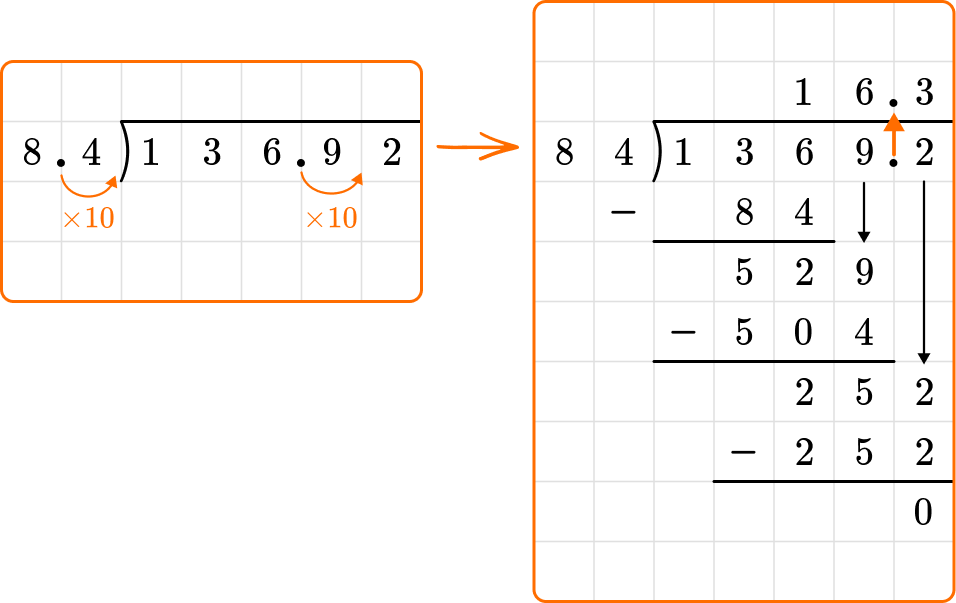
5. Solve 136.92 \div 8.4

Since the divisor is a decimal, first you need to multiply it by a power of 10 to make it a whole number. Since there is one decimal place, you can multiply it by 10 to make it a whole number. Then, you need to multiply the dividend by the same number before beginning the long division process.

6. Solve 9 \div \cfrac{1}{3} .

To solve, take the reciprocal of the divisor and then change to multiplication.

7. Solve \cfrac{3}{8} \div 6. Simplify your answer.

\cfrac{3}{48} can be simplified to \cfrac{1}{16}.

Since the directions specify that the answer must be simplified, the correct answer is \cfrac{1}{16}.

8. Solve \cfrac{5}{6} \div \cfrac{2}{3}. Simplify your answer.

\cfrac{15}{12} can be simplified to \cfrac{5}{4} then simplified again to 1 \cfrac{1}{4} \, .

Since the directions specify that the answer must be simplified, the correct answer is 1 \cfrac{1}{4}.

Division FAQs

Division is a mathematical operation that involves splitting a quantity into equal parts or groups, or determining how many times one number (the divisor) is contained within another number (the dividend). The result of division is called the quotient.

Division by zero is “undefined.” This means that it is not possible to divide any number by zero and get a meaningful result.

The division operation is represented by a horizontal line with a dot above and below it called an obelus (\div). It can also be represented by a forward slash (/).

The next lessons are

• Types of numbers
• Rounding numbers
• Factors and multiples

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

Division Word Problems (1-step word problems)

In these lessons, we will learn to solve word problems involving division.

Related Pages 2-Step Division Word Problems More Word Problems More Singapore Math Lessons

Here are some examples of division word problems that can be solved in one step. We will illustrate how block diagrams or tape diagrams can be used to help you to visualize the division word problems in terms of the information given and the data that needs to be found.

We use division or multiplication when the problem involves equal parts of a whole. The following diagram shows how to use division to find unknown size of parts or groups or to find unknown number of parts or groups. Scroll down the page for examples and solutions.

Example: There are 160 grade 3 students in a school. The students are to be equally divided into 5 classes. How many students do we have in each class?

160 ÷ 5 = 32

We have 32 students in each class.

Example: Melissa made 326 cupcakes. She packed 4 cupcakes into each box. How many boxes of cupcakes did she pack? How many cupcakes were left unpacked?

326 ÷ 4 = 81 remainder 2

She packed 81 boxes of cupcakes.

2 cupcakes were left unpacked.

How to solve multiplication and division problems by drawing a diagram? Division: Finding the Number in Each Group

Example: Victor opened a bag of pretzels and counted 56. He gave each of 7 friends an equal number of pretzels. How many pretzels did each friend receive?

Use Tape Diagrams to solve Word Problems with Unknown Number of Groups

Example: A vet gives the dogs in her office 4 bones each. She used 24 bones. How many dogs got bones?

Tape Diagrams - Unknown Size of Groups How to make a tape diagram to solve a word problem with an unknown size of groups?

Example: Mrs. Silverglat has 21 pretzels. She gives seven students am equal amount of pretzels. How many pretzels does each student get?

Practice solving the following multiplication and division word problems.

• Dan went to the market on Friday. He bought two tomatoes. On Sunday, he bought six times as many. How many tomatoes did he buy on Sunday?
• In July, a construction company built 360 miles of road. In February, the company laid down 60 miles of road. How many times more road did the company complete in July?
• Linh ran 21 miles. Linh ran three times as far as Sophie. How far did Sophie run?
• Molly’s bedroom is 220 square feet. Molly’s dining room is five times the size of her bedroom. How large is her dining room?

Using Division Tape Diagrams to find Unknown Number of Groups

Example: After playing Belmont, the 24 Islander players traveled to South Boston. This time they went by car and 3 players rode in each care. How many cars did they need?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.